2018年AMC 10B试题/第1题
问题
凯特烤制了一盘20英寸×18英寸的玉米面包。将玉米面包切成边长为2英寸的小方块,这盘玉米面包共可切出多少块?
(A) 90 (B) 100 (C) 180 (D) 200 (E) 360
解决方案 1
平底锅的面积为 \( {20} \cdot {18} = {360} \) 。由于每块面积为4,因此共有 \( \frac{360}{4} = {90} \) 块。所以,答案是 \( A \) 。
解决方案 2
将每个维度除以2,我们得到一个 \( {10} \times 9 \) 网格,共90块。因此,答案是 \( \bar{A} \)
2018 AMC 10B 试题/第2题
问题
萨姆在90分钟内行驶了96英里。他在前30分钟内的平均速度为 \( {60}\mathrm{{mph}} \) (英里/小时),在接下来的30分钟内的平均速度为 \( {65}\mathrm{{mph}} \) 。那么,他在最后30分钟内的平均速度是多少(英里/小时)?
(A) 64 (B) 65 (C) 66 (D) 67 (E) 68
解决方案
让萨姆在前半小时以精确的60英里/小时(60mph)行驶,在第二个半小时以65英里/小时(65mph)行驶,在第三个半小时以 \( x \) 英里/小时行驶。由于 \( {rt} = d \) ,且30分钟等于半小时,他在前30分钟内行驶了 \( {60} \cdot \frac{1}{2} = {30} \) 英里。
同样地,他在第二个半小时内行驶了 \( \frac{65}{2} \) 英里。
题目说萨姆在90分钟内行驶了96英里,这意味着他必定已经行驶了
\( {96} - \left( {{30} + \frac{65}{2}}\right) = {33}\frac{1}{2} \) 英里在第三个半小时时段内。
\[ {rt} = d,\text{ so }x \cdot \frac{1}{2} = {33}\frac{1}{2}. \]
因此,Sam 在第三个半小时以 (D) 67 英里/小时的速度行驶。
2018 AMC 10B 试题/第 3 题
题目
在表达式 \( \left( {\underline{\;} \times \underline{\;}}\right) + \left( {\underline{\;} \times \underline{\;}}\right) \) 中,每个空白处需填入数字 1、2、3 或 4 中的一个,且每个数字只能使用一次。可以得到多少个不同的值?
(A) 2 (B) 3 (C) 4 (D) 6 (E) 24
解答
我们有 \( \left( \begin{array}{l} 4 \\ 2 \end{array}\right) \) 种方式选择配对,并且值可以互换,因此有 2 种方式,所以 \( \frac{6}{2} = \) 3。
解答 2
我们有四个可用数字(1,2,3,4)。由于不同排列无关紧要,因为都是加法和乘法,如果我们把 1 放在第一个空格,显然有 [3] 种可能结果(2,3,4)。
解答 3
有 \( 4! \) 种方式排列这些数字,由于交换律,每种方式会重复计数 \( 2!2!2! \) 次。因此,答案是 \( \frac{4!}{2!2!2!} = 3 \)
2018 AMC 10B 试题/第 4 题
题目
一个三维长方体盒子,其尺寸分别为 \( X \) 、 \( Y \) 和 \( Z \) ,其六个面的表面积分别为 24、24、48、48、72 和 72 平方单位。求 \( X \) + \( Y \) + \( Z \) 的值?
(A) 18 (B) 22 (C) 24 (D) 30 (E) 36
解法1
设 \( X \) 为最短边的长度, \( Z \) 为最长边的长度。于是 \( {XY} = {24} \) 、 \( {YZ} = {72} \) 和 \( {XZ} = {48} \) 。将前两个方程相除得 \( \frac{Z}{X} = 3 \) 。再乘以最后一个方程得 \( {Z}^{2} = {144} \) ,从而 \( Z = {12} \) 。接着 \( X = 4 \) 且 \( Y = 6 \) 。
最终答案为 \( 4 + 6 + {12} = {22} \) 。 \( B \)
解法2
直接通过试算可知尺寸为4×6×12,因此答案为 \( 4 + 6 + {12} = {22} \) 。 \( B \)
解法3
若求24、48、72的最大公约数(GCD),可得第一个数12。接着做 \( {48} \div {12} \) 和 \( {72} \div {12} \) 得到4和6,即另外两个数。将这三个数相加得22,即 \( B \) 。
2018 AMC 10B 试题/第5题
题目
\( \{ 2,3,4,5,6,7,8,9\} \) 的子集中有多少个至少包含一个质数?
(A) 128 (B) 192 (C) 224 (D) 240 (E) 256
解法1
考虑计算不含任何质数的子集数量。集合中有四个质数:2、3、5、7。因此不含任何质数的子集数量等于 \( \{ 4,6,8,9\} \) 的子集数,即 \( {2}^{4} = {16} \) 。至少含一个质数的子集数等于总子集数减去不含任何质数的子集数。有理由的子集数为256-16,故答案为 \( {256} - {16} = 0 \) 。
解法2(利用选项)
共有4个合数,可分别列出1个数、2个数、3个数、4个数的形式。现在可用排列
\( \left( \begin{array}{l} 4 \\ 1 \end{array}\right) + \left( \begin{array}{l} 4 \\ 2 \end{array}\right) + \left( \begin{array}{l} 4 \\ 3 \end{array}\right) + \left( \begin{array}{l} 4 \\ 4 \end{array}\right) = {15} \) 。根据选项,唯一15的倍数是
2018年AMC 10B试题/第6题
一个盒子中有5枚筹码,分别编号为1、2、3、4、5。每次随机抽取一枚且不放回,直到已抽出的数值之和超过4为止。求恰好需要抽取3次的概率。
(A) \( \frac{1}{15} \) (B) \( \frac{1}{10} \) (C) \( \frac{1}{6} \) (D) \( \frac{1}{5} \) (E) \( \frac{1}{4} \)
解决方案 1
注意到,仅需不超过两次抽取的仅有四种情况为1,2;1,3;2,1;以及3,1。注意每种情况的概率均为 \( \frac{1}{5} \cdot \frac{1}{4} \) ,因此答案为 \( \frac{1}{5} \cdot \frac{1}{4} \cdot 4 = \frac{1}{5} \) ,即D。
解决方案2
注意只有前两次抽取才重要,第三次抽到什么数字无关紧要,因为无论抽到怎样的3个数字组合,其和必定大于5。还需注意,为了凑齐3次抽取,必须抽到1,否则在两次或更少抽取内就能达到5。因此抽到1的概率是 \( \frac{1}{5} \) 。接下来必须抽到2或3,其概率为 \( \frac{1}{2} \) 。但抽取顺序可以互换,于是得到:
\[ \frac{1}{5} \cdot \frac{1}{2} \cdot 2 = \frac{1}{5}\text{ or }D \]
作者:Soccer_JAMS
2018年AMC 10B试题/第7题
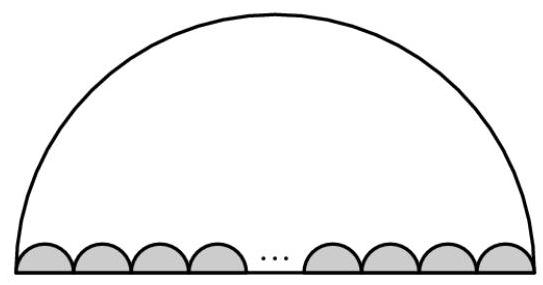
在下图中, \( N \) 个全等半圆(congruent semicircles)位于一个大半圆的直径上,它们的直径无重叠地覆盖了大半圆的整个直径。设 \( A \) 为小半圆的总面积, \( B \) 为大半圆内部但位于小半圆外部的区域面积。比值 \( A : B \) 为 \( 1 : {18} \) 。 \( N \) 是多少?
(E) 36
解法1(利用选项进行计算)
使用给出的选项进行计算,能成立的是D
解法2(更具代数性的方法)
设半圆的数量为 \( n \) ,每个半圆的半径为 \( r \) 。为求所有小半圆的总面积,我们有 \( n \cdot \frac{\pi \cdot {r}^{2}}{2} \) 。
接下来,我们需要求出大半圆的面积。大半圆的半径可推得为 \( n \cdot r \) 。因此,大半圆的面积为 \( \frac{\pi \cdot {n}^{2} \cdot {r}^{2}}{2} \) 。
既然我们已经求出了A和B的面积,就可以求出它们的比值。 \( \frac{A}{B} = \frac{1}{18} \) ,因此部分与整体的比值为 \( 1 : {19} \) 。当我们把小半圆的总面积除以大半圆的总面积时,得到 \( \frac{1}{n} \) 。这等于 \( \frac{1}{19} \) 。令两者相等,我们得到 \( n = {19} \) 。这就是我们的答案,对应选项 \( 0\mathrm{O}{19} \) 。解法作者:Archimedes15
解法3
每个小半圆是大半圆的 \( \frac{1}{{N}^{2}} \) 。因为 \( N \) 个小半圆构成大半圆的 \( \frac{1}{19} \) ,所以 \( \frac{N}{{N}^{2}} = \frac{1}{19} \) 。解得19。另见
2018 AMC 10B 试题/第8题
萨拉用牙签搭出如下所示的阶梯:

这是一个3级阶梯,共用了18根牙签。如果一个阶梯用了180根牙签,那么它有多少级?
(A) 10 (B) 11 (C) 12 (D) 24 (E) 30 目录 - 1 解法 - 2 解法2 - 3 解法3 - 4 另见
解法
一个有 \( n \) 级的阶梯包含 \( 4 + 6 + 8 + \ldots + {2n} + 2 \) 根牙签。这可改写为 \( \left( {n + 1}\right) \left( {n + 2}\right) - 2 \) 。
所以, \( \left( {n + 1}\right) \left( {n + 2}\right) - 2 = {180} \)
所以, \( \left( {n + 1}\right) \left( {n + 2}\right) = {182} \) 。
通过观察可知 \( {13} * {14} = {182} \) ,因此答案为 \( {13} - 1 = {(C)12} \)
解法2
第1层:4级
第 \( 1,2:{10} \) 层:级
第1,2,3层:18级
第1,2,3,4层:28级
通过观察可以发现,每增加一层,当前层与上一层牙签数量的差值增加2。利用这一规律:
4,10,18,28,40,54,70,88,108,130,154,180
由此可知,解确实为 \( {(C)12} \)
作者:Soccer_JAMS
2018 AMC 10B 第9题
7颗标准骰子的每个面分别标有1到6的整数。设 \( p \) 为掷出这7颗骰子时,顶面数字之和为10的概率。问还有哪个和与 \( p \) 的概率相同?
(A) 13 (B) 26 (C) 32 (D) 39 (E) 42
解法1
可以看出,掷出最小可能数的概率与掷出最大可能数的概率相同;掷出第二小可能数的概率与掷出第二大可能数的概率相同,以此类推。这是因为将若干1加到7个1的组合数,与从7个6中减去若干1的组合数相同。
因此,我们可以配对找出与10概率相同的和。首先注意到7是最小可能掷出值,42是最大可能掷出值。概率相同的配对如下:
\( \left( {7,{42}}\right) ,\left( {8,{41}}\right) ,\left( {9,{40}}\right) ,\left( {{10},{39}}\right) ,\left( {{11},{38}}\right) \ldots \)
然而,我们需要找到与10配对的数。因此,我们可以在(10, 39)处停止,并推断出与10概率相同的和为39。所以正确答案是(D,39),解答完毕。
作者:Archimedes15
解法2
设未知值为 \( x \) 。根据对称性,我们意识到10与最小掷出值之差等于最大掷出值与 \( x \) 之差。因此,
\( {10} - 7 = {42} - x \)
\( x = {39} \) ,答案为(D)39| 作者:Soccer_JAMS
解法3(简单逻辑)
要使和具有相同概率,两组7颗骰子的平均和必须为 \( \left( {6 + 1}\right) \times 7 = {49} \) 。由于出现10与不出现10对称,只需用期望总和减去10。49 - 10 = 39,因此答案为 \( \left| \mathbf{\left( D\right) {39}}\right| \)
作者:epicmonster
解法4
骰子点数总和的期望值为 \( {3.5} * 7 = {24.5} \) ,由于概率应在24.5两侧对称分布,故答案为 \( {24.5} + {24.5} - {10} = {39} \) ,即 \( \left| {\mathbf{\left( D\right) }{39}}\right| \) 。
作者:dajeff
注记
计算总和为10的概率同样简单。共有3种情况:
2018 AMC 10B 试题/第10题
题目
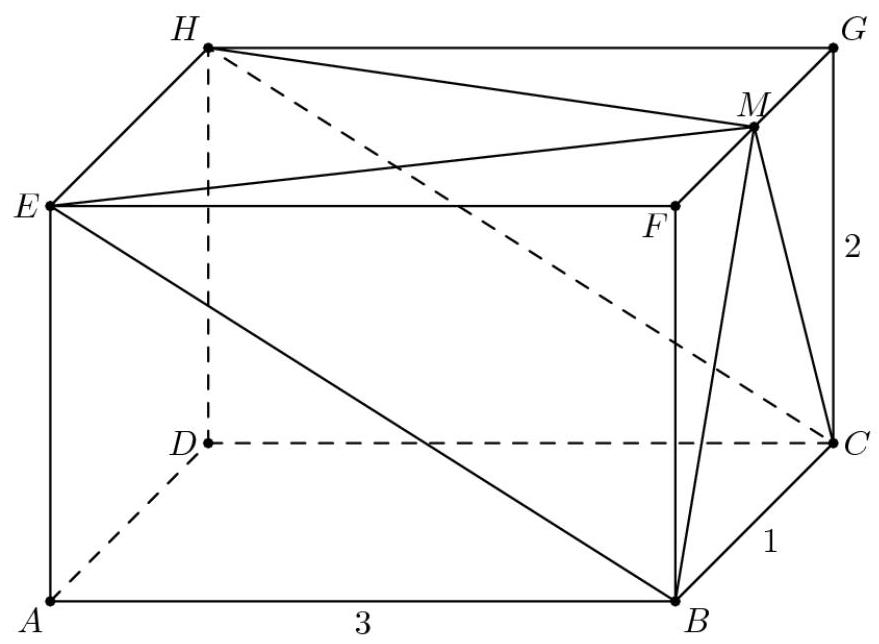
在所示的长方体(rectangular parallelepiped)中, \( {AB} = 3 \) 、 \( {BC} = 1 \) 和 \( {CG} = 2 \) 。点 \( M \) 为 \( \overline{FG} \) 的中点。以 \( {BCHE} \) 为底、 \( M \) 为顶点的长方锥体积是多少?(A) 1 (B) \( \frac{4}{3} \) (C) \( \frac{3}{2} \) (D) \( \frac{5}{3} \) (E) 2
解法1
考虑横截面并设其面积为 \( b \) 。注意包围该锥体的三棱柱体积为 \( {bh}/2 = 3 \) ,而我们要求的是与该三棱柱同底同高的长方锥。该锥体体积为 \( {bh}/3 \) ,故答案为2
解法2
首先求出整个平行六面体的体积。由于长方体(rectangular parallelepiped)即长方体,其体积为 \( 2 \cdot 3 \cdot 1 = 6 \) 。
接着考虑平面 \( {BCHE} \) 切割图形后形成的楔形体。可求以EFB为底、M为顶点的三棱锥体积。EFB的面积为 \( \frac{1}{2} \cdot 2 \cdot 3 = 3 \) 。已知BC=1,故FM= \( \frac{1}{2} \) 。利用三棱锥体积公式得 \( V = \frac{1}{3} \cdot \frac{1}{2} \cdot 3 = \frac{1}{2} \) 。同理,以HGC为底、M为顶点的三棱锥尺寸完全相同,其体积亦为 \( \frac{1}{2} \) 。
2018 AMC 10B 试题/第11题
当 \( p \) 为质数时,下列哪个表达式永远不是质数?
(A) \( {p}^{2} + {16} \) (B) \( {p}^{2} + {24} \) (C) \( {p}^{2} + {26} \) (D) \( {p}^{2} + {46} \) (E) \( {p}^{2} + {96} \)
解法1
因为非3的倍数的平方总是 \( 1{\;\operatorname{mod}\;3} \) ,唯一总是3的倍数的表达式是(C) \( {p}^{2} + {26} \) 。这排除了 \( p = 0{\;\operatorname{mod}\;3} \) 的情况,而这种情况仅当 \( p = 3 \) 时发生,此时 \( {p}^{2} + {26} = {35} \) 仍为合数。
解法2(不推荐)
我们采用试数法:
\( {5}^{2} + {16} = {41}\;{7}^{2} + {24} = {73}\;{5}^{2} + {46} = {71}\;{19}^{2} + {96} = {457} \) 。显然只有(C)是剩下的唯一选项。(franchester)
解法3
质数只能为1或 \( - 1{\;\operatorname{mod}\;6} \) 。因此,质数的平方只能为 \( 1{\;\operatorname{mod}\;6} \) 。 \( {p}^{2} + {26} \) 于是必为 \( 3{\;\operatorname{mod}\;6} \) ,所以它总能被3整除。因此答案为(C)。
2018 AMC 10B 试题/第12题
线段 \( \overline{AB} \) 是直径为 \( {AB} = {24} \) 的圆的直径。点 \( C \) ,既不等于 \( A \) 也不等于 \( B \) ,位于圆上。当点 \( C \) 在圆上移动时, \( \bigtriangleup {ABC} \) 的重心(质心)描绘出一条缺少两点的闭合曲线。该曲线所围区域的面积最接近的正整数是多少?
(A) 25 (B) 38 (C) 50 (D) 63 (E) 75
解法
设 \( A = \left( {-{12},0}\right) , B = \left( {{12},0}\right) \) 。因此, \( C \) 位于方程为 \( {x}^{2} + {y}^{2} = {144} \) 的圆上。设其坐标为(x, y)。由于我们知道顶点坐标为 \( \left( {{x}_{1},{y}_{1}}\right) ,\left( {{x}_{2},{y}_{2}}\right) ,\left( {{x}_{3},{y}_{3}}\right) \) 的三角形的重心为 \( \left( {\frac{{x}_{1} + {x}_{2} + {x}_{3}}{3},\frac{{y}_{1} + {y}_{2} + {y}_{3}}{3}}\right) \) , \( \bigtriangleup {ABC} \) 的重心为 \( \left( {\frac{x}{3},\frac{y}{3}}\right) \) 。因为 \( {x}^{2} + {y}^{2} = {144} \) ,我们知道 \( {\left( \frac{x}{3}\right) }^{2} + {\left( \frac{y}{3}\right) }^{2} = {16} \) ,所以该曲线是以原点为圆心的圆。因此,其面积为 \( {16\pi } \approx \left( \mathrm{C}\right) {50} \) 。 -tdeng
解法2(无坐标)
我们知道三角形的重心将中线分为2:1的两段,而三角形中通向圆心的中线即为半径(长度为12),因此三角形的重心到圆心的距离恒为 \( \frac{1}{3} \cdot {12} = 4 \) 。半径为4的圆的面积为 \( {16\pi } \) ,约等于 \( \mathrm{{CC}} \) ) 50。That_Crazy_Book_Nerd
2018 AMC 10B 试题/第13题
问题
在序列 \( {101},{1001},{10001},{100001},\ldots \) 的前2018个数中,有多少个能被101整除?
(A) 253 (B) 504 (C) 505 (D) 506 (E) 1009
解答
注意到对于某个奇数 \( k \) , \( {\underline{10}}^{2k} + 1 \) 即可满足 \( {\;\operatorname{mod}\;{10}}1 \) 。每个 \( {2k} \in \{ 2,4,6,\ldots ,{2018}\} \) ,因此答案是(C) 505 (AOPS12142015)
解答2
若将每个数除以101,可观察到每4个数出现一个模式。 \( {101},{1000001},{10000000001},\ldots \) 。我们将2018除以4得到504余2。余下的2个数中有一个可被整除,因此答案为(C) 505
解答3
注意到909能被101整除,因此9999也能。已知101可被整除而1001不能,故从10001开始。我们减去9999得2。同理,从100001减去,但改为减去9999×10即99990得11。再次操作,将9的个数乘以10得101。依此规律,可用模101完成本题。序列即减1、乘10再加1。因此序列 \( 0, - 9, - {99}\left( 2\right) ,{11},0,\ldots \) ,每4项循环。从第1项后考虑,共2017个数。2017除以4得504余1,故答案为504加第1项,即(C) 505
-googleghosh
2018 AMC 10B 第14题
一个包含2018个正整数的列表有唯一众数,该众数恰好出现10次。列表中至少有多少个不同的取值?
(A) 202 (B) 223 (C) 224 (D) 225 (E) 234
解答
为使取值数量最少,需最大化每个取值的重复次数。因此,可让223个数各出现9次,1个数出现1次,众数出现10次,总计 \( {223} + 1 + 1 \) =
(D) 225
2018 AMC 10B 第15题
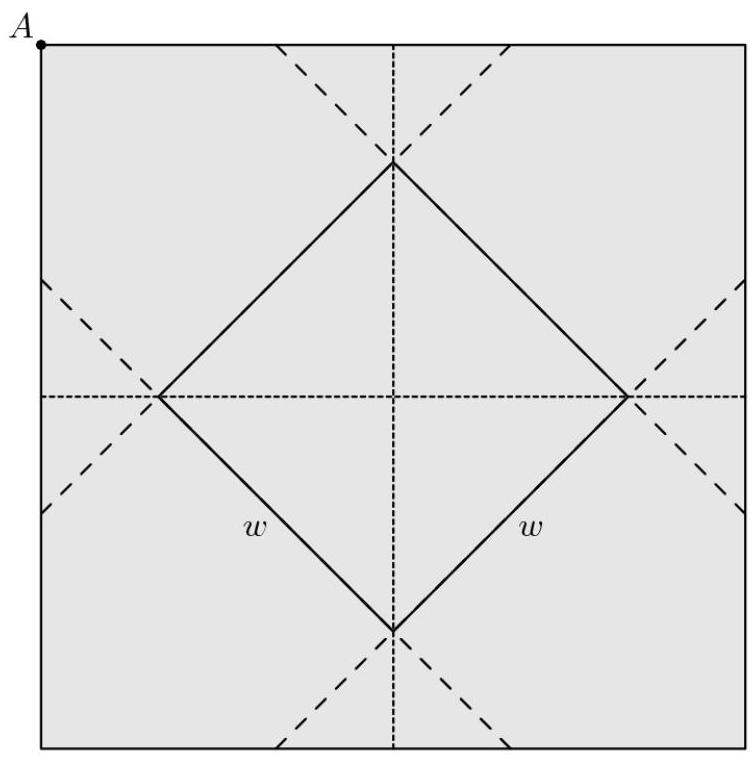
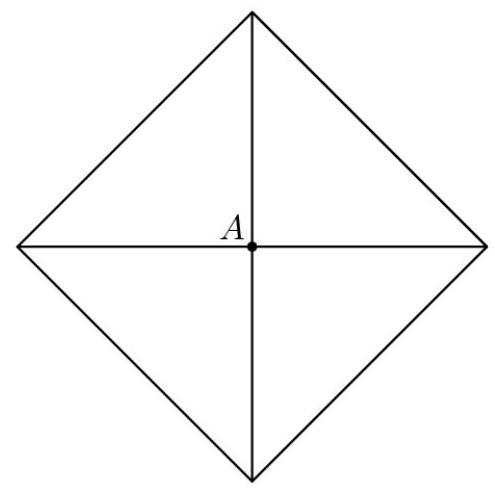
一个底面为正方形的封闭盒子要用一张正方形包装纸包裹。盒子居中放在包装纸上,其底面的四个顶点落在正方形包装纸中线的中点,如左图所示。包装纸的四个角向上折起,沿盒子的侧面汇聚到盒子顶面的中心点,即右图中的点 \( A \) 。盒子的底边长为 \( w \) ,高为 \( h \) 。求这张包装纸的面积。
(A) \( 2{\left( w + h\right) }^{2} \) (B) \( \frac{{\left( w + h\right) }^{2}}{2} \) (C) \( 2{w}^{2} + {4wh} \) (D) \( 2{w}^{2} \) (E) \( {w}^{2}h \) 解法1
考虑图像的四分之一(包装纸被分成4个全等正方形)。每条虚线的长度为 \( h \) 。长为 \( w \) 、宽为 \( h \) 的矩形面积为 \( {wh} \) 。两个以 \( h \) 为底的三角形组合成一个以 \( h \) 为对角线的正方形。根据勾股定理(Pythagorean Theorem),该正方形的每条边长为 \( \sqrt{\frac{{h}^{2}}{2}} \) ,因此面积为边长的平方,即 \( \frac{{h}^{2}}{2} \) 。同理,两个以 \( w \) 为底的三角形组合成一个面积为 \( \frac{{w}^{2}}{2} \) 的正方形。将以上所有面积相加,得到 \( \frac{{w}^{2}}{2} + \frac{{h}^{2}}{2} + {wh} \) 。由于整张包装纸包含4个这样的区域,我们将其乘以4,得到 \( 4\left( {\frac{{w}^{2}}{2} + \frac{{h}^{2}}{2} + {wh}}\right) = 2\left( {{w}^{2} + {h}^{2} + {2wh}}\right) = 4{\left( A\right) }^{2}{\left( w + h\right) }^{2} \)
解决方案 2
这张纸的面积由盒子的表面积加上四个三角形的面积组成。表面积为 \( 2{w}^{2} + {2wh} + {2wh} \) ,等于 \( 2{w}^{2} + {4wh} \) 。四个三角形的高和底均为 \( h \) ,因此每个三角形的面积为 \( \frac{{h}^{2}}{2} \) 。共有四个,所以乘以四得 \( 2{h}^{2} \) 。因此,纸张的总面积为 \( 2{w}^{2} + {4wh} + 2{h}^{2} \) 。该式可因式分解并写作 \( \Delta {\left( \mathbf{A}\right) }^{2}{\left( w + h\right) }^{2} \) 。另见
2018年AMC 10B试题/第16题
设 \( {a}_{1},{a}_{2},\ldots ,{a}_{2018} \) 为一个严格递增的正整数序列,满足
\[ {a}_{1} + {a}_{2} + \cdots + {a}_{2018} = {2018}^{2018}. \]
\( {a}_{1}^{3} + {a}_{2}^{3} + \cdots + {a}_{2018}^{3} \) 除以 6 的余数是多少?
\( \textbf{(A)}\;0\;\textbf{(B)}\;1\;\textbf{(C)}\;2\;\textbf{(D)}\;3\;\textbf{(E)}\;4 \)
解决方案 1
可以简单地把所有数的三次剩余列出来 \( \;\mathrm{{mod}}\;6 \) 。(编辑:欧拉φ定理(Euler’s totient theorem)并不能用来证明它们全都同余 \( \;\mathrm{{mod}}\;6 \) ,因为 \( {a}_{k} \) 不一定与6互质。)
因此答案与 \( {2018}^{2018} \equiv {2}^{2018}\left( {\;\operatorname{mod}\;6}\right) = 0\;{.6} \) 同余
解决方案 2
(不怎么样)
注意 \( {\left( {a}_{1} + {a}_{2} + \cdots + {a}_{2018}\right) }^{3} = {a}_{1}^{3} + {a}_{2}^{3} + \cdots + {a}_{2018}^{3} + 3{a}_{1}^{2}\left( {{a}_{1} + {a}_{2} + \cdots + {a}_{2018} - {a}_{1}}\right) + 3{a}_{2}^{2}\left( {{a}_{1} + {a}_{2} + \cdots + {a}_{2018} - {a}_{2}}\right) + \cdots + \) \( 3{a}_{2018}^{2}\left( {{a}_{1} + {a}_{2} + \cdots + {a}_{2018} - {a}_{2018}}\right) + 6\mathop{\sum }\limits_{{i \neq j \neq k}}^{{2018}}{a}_{i}{a}_{j}{a}_{k} \)
\( \begin{array}{l} \text{ Note that } \\ {a}_{1}^{3} + {a}_{2}^{3} + \cdots + {a}_{2018}^{3} + 3{a}_{1}^{2}\left( {{a}_{1} + {a}_{2} + \cdots + {a}_{2018} - {a}_{1}}\right) + 3{a}_{2}^{2}\left( {{a}_{1} + {a}_{2} + \cdots + {a}_{2018} - {a}_{2}}\right) + \cdots + 3{a}_{2018}^{2}\left( {{a}_{1} + {a}_{2} + \cdots + {a}_{2018} - {a}_{2018}}\right) + \end{array} \)
\( 6\mathop{\sum }\limits_{{i \neq j \neq k}}^{{2018}}{a}_{i}{a}_{j}{a}_{k} \equiv {a}_{1}^{3} + {a}_{2}^{3} + \cdots + {a}_{2018}^{3} + 3{a}_{1}^{2}\left( {{2018}^{2018} - {a}_{1}}\right) + 3{a}_{2}^{2}\left( {{2018}^{2018} - {a}_{2}}\right) + \cdots + 3{a}_{2018}^{2}\left( {{2018}^{2018} - {a}_{2018}}\right) \equiv - 2({a}_{1}^{3} + {a}_{2}^{3} + \cdots + {a}_{2018}^{3} \)
(模6)
因此, \( - 2\left( {{a}_{1}^{3} + {a}_{2}^{3} + \cdots + {a}_{2018}^{3}}\right) \equiv {\left( {2018}^{2018}\right) }^{3} \equiv {\left( {2}^{2018}\right) }^{3} \equiv {4}^{3} \equiv 4\left( {\;\operatorname{mod}\;6}\right) \) 。
于是, \( {a}_{1}^{3} + {a}_{2}^{3} + \cdots + {a}_{2018}^{3} \equiv 1{\;(\operatorname{mod}\;3)} \) 。然而,由于立方运算保持奇偶性,且各项之和为偶数,故这些立方数之和亦为偶数,且
我们的答案为 \( \left( \mathrm{E}\right) 4 \)
解法3
我们首先注意到 \( {1}^{3} + {2}^{3} + \ldots = {\left( 1 + 2 + \ldots \right) }^{2} \) 。因此,我们要求的是 \( {\left( {2018}^{2018}\right) }^{2} = \left( {2018}^{4036}\right) \) 模6的值。首先,2018与2模6同余。于是,我们要求的是 \( \left( {2}^{4036}\right) \) 模6的值。与其用数论技巧,不如直接寻找规律。从2的较小次幂开始,我们发现 \( {2}^{1} \) 模6为2, \( {2}^{2} \) 模6为4, \( {2}^{3} \) 模6为2, \( {2}^{4} \) 模6为4,依此类推……因此,由于 \( \left( {2}^{4036}\right) \) 的指数为偶数,它必与4模6同余,从而得到答案(E) 4。你可以用模运算证明这一规律,但我觉得这样更简单。
TheMagician
解法4(偷懒解法)
假设 \( {a}_{1},{a}_{2},\ldots {a}_{2017} \) 均为6的倍数,并求出 \( {2018}^{2018}\;\left( {\operatorname{mod}\;6}\right) \) (恰好为4)。于是 \( {a}_{1}{}^{3} + \ldots + {a}_{2018}{}^{3} \) 与 \( {64}{\;(\operatorname{mod}\;6)} \) 同余,即4。——Patrick4President
解法5(费马小定理)
首先注意,根据费马小定理(Fermat’s Little Theorem),每个 \( {a}_{i}^{3} \equiv {a}_{i}{\;(\operatorname{mod}\;3)} \) 。这意味着 \( {a}_{1}^{3} + \) … \( + {a}_{2018}^{3} \equiv {a}_{1} + \) … \( + {a}_{2018} \equiv {2}^{2018} \equiv 1{\;(\operatorname{mod}\;3)} \) 。此外,所有 \( {a}_{i}^{2} \equiv {a}_{i}\left( {\;\operatorname{mod}\;2}\right) \) ,因此根据费马小定理, \( {a}_{i}^{3} \equiv \left( {a}_{i}\right) \left( {a}_{i}^{2}\right) \equiv {a}_{i}^{2} \equiv {a}_{i}{\;(\operatorname{mod}\;2)} \) 。于是 \( {a}_{1}^{3} + \ldots {a}_{2018}^{3} \equiv {2}^{2018} \equiv 0{\;(\operatorname{mod}\;2)} \) 。现在设 \( x = {a}_{1}^{3} + \ldots + {a}_{2018}^{3} \) 。那么我们有同余式 \( x \equiv 0{\;(\operatorname{mod}\;2)} \) 和 \( x \equiv 1{\;(\operatorname{mod}\;3)} \) 。根据中国剩余定理(Chinese Remainder Theorem),解一定存在,并且解同余式后我们得到 \( x \equiv 4{\;(\operatorname{mod}\;6)} \) 。因此答案为 \( \left( E\right) 4 \)
2018 AMC 10B 试题/第17题
题目
在矩形 \( {PQRS} \) 中, \( {PQ} = 8 \) 且 \( {QR} = 6 \) 。点 \( A \) 和 \( B \) 位于 \( \overline{PQ} \) 上,点 \( C \) 和 \( D \) 位于 \( \overline{QR} \) 上,点 \( E \) 和 \( F \) 位于 \( \overline{RS} \) 上,点 \( G \) 和 \( H \) 位于 \( \overline{SP} \) 上,使得 \( {AP} = {BQ} < 4 \) 且凸八边形
\( {ABCDEFGH} \) 为等边。该八边形的一条边长可表示为 \( k + m\sqrt{n} \) ,其中 \( k \) 、 \( m \) 和 \( n \) 为整数,且 \( n \) 不被任何素数的平方整除。 \( k + m + n \) 是多少?
(A) 1 (B) 7 (C) 21 (D) 92 (E) 106
解法1
设 \( {AP} = {BQ} = x \) 。则 \( {AB} = 8 - {2x} \) 。
现在注意到,由于 \( {CD} = 8 - {2x} \) ,我们有 \( {QC} = {DR} = x - 1 \) 。
因此,根据勾股定理(Pythagorean Theorem),我们有 \( {x}^{2} + {\left( x - 1\right) }^{2} = {\left( 8 - 2x\right) }^{2} \) ,即
\( 2{x}^{2} - {30x} + {63} = 0 \Rightarrow x = \frac{{15} - 3\sqrt{11}}{2}. \)
我们的答案是 \( 8 - \left( {{15} - 3\sqrt{11}}\right) = 3\sqrt{11} - 7 \Rightarrow \) (B) 7。(Mudkipswims42)
解法2
记等边八边形的边长为 \( x \) 。 \( \overline{BQ} \) 的长度可表示为 \( \frac{8 - x}{2} \) 。根据勾股定理,我们得到:
\[ {\left( \frac{8 - x}{2}\right) }^{2} + {\overline{CQ}}^{2} = {x}^{2} \Rightarrow \overline{CQ} = \sqrt{{x}^{2} - {\left( \frac{8 - x}{2}\right) }^{2}} \]
由于 \( \overline{CQ} = \overline{DR} \) ,我们可以说 \( x + 2\sqrt{{x}^{2} - {\left( \frac{8 - x}{2}\right) }^{2}} = 6 \Rightarrow x = - 7 \pm 3\sqrt{11} \) 。我们可以舍去负解,因此 \( k + m + n = - 7 + 3 + {11} = \) (B)7 - blitzkrieg21
2018年AMC 10B试题/第18题
来自不同家庭的三对兄妹需要乘坐一辆面包车出行。这六个孩子将占据面包车的第二排和第三排,每排各有三个座位。为避免干扰,兄妹不得在同一排相邻而坐,且任何孩子不得直接坐在其兄妹的正前方。问:此次出行共有多少种可能的座位安排?
(A) 60 (B) 72 (C) 92 (D) 96 (E) 120
解法1(分类讨论)
我们可以开始分情况讨论。将这三对分别称为 \( a \) 、 \( b \) 和 \( c \) ,并假设 \( a \) 中的一位坐在第二排最左侧的座位上。于是可得到以下情况。
案例1:第二行:a b c 第三行:b c a
案例2:第二行:a c b 第三行:c b a
案例3:第二行:a b c 第三行:c a b
案例4:第二行:a c b 第三行:b a c
对于四种情况中的每一种,我们都可以交换兄弟姐妹的位置,因为他们是不同的个体。因此,每种情况都有 \( 2 \cdot 2 \cdot 2 = 8 \) 种可能性。由于共有四种情况,当配对 \( a \) 中有人坐在第二排最左侧座位时,共有32种重新排列方式。然而,来自配对 \( a \) 、 \( b \) 或 \( c \) 中的任意一人都有可能坐在第二排最左侧座位。因此,我们需要乘以3,得到最终答案 \( {32} \cdot 3 = {96} \) 。所以,正确答案是 \( \mid \left( \mathbf{D}\right) {96} \mid \) 。
作者:Archimedes15
解法2
将兄弟姐妹称为 \( {A}_{1},{A}_{2},{B}_{1},{B}_{2},{C}_{1} \) 和 \( {C}_{2} \) 。
第一个座位有6种选择,具体由哪个孩子坐并不重要,因此不失一般性假设 \( {A}_{1} \) 坐在这里( \( \circ \) 为空座位):
\( {A}_{1} \circ \circ \)
O O O
接着第二个座位有4种选择( \( {B}_{1} \) 、 \( {B}_{2} \) 、 \( {C}_{1} \) 或 \( {C}_{2} \) )。同样,谁坐这里并不重要,因此WLOG假设是 \( {B}_{1} \) :
\( {A}_{1}{B}_{1} \circ \)
O O O
第一排最后一个座位不能是 \( {A}_{2} \) ,否则无法构造出满足条件的第二排。因此,它必须是 \( {C}_{1} \) 或 \( {C}_{2} \) 。WLOG假设是 \( {C}_{1} \) 。构造第二排有两种方式:
\( {A}_{1}{B}_{1}{C}_{1} \)
\( {B}_{2}{C}_{2}{A}_{2} \)
\( {A}_{1}{B}_{1}{C}_{1} \)
\( {C}_{2}{A}_{2}{B}_{2} \)
作者:R1ceming
2018 AMC 10B 试题/第19题
题目
乔伊(Joey)、克洛伊(Chloe)和他们的女儿佐伊(Zoe)三人生日相同。乔伊比克洛伊大1岁,而佐伊今天正好1岁。今天是克洛伊的年龄首次成为佐伊年龄整数倍的9个生日中的第一个。下一次乔伊的年龄是佐伊年龄整数倍时,乔伊年龄的两位数字之和是多少?
(A) 7 (B) 8 (C) 9 (D) 10 (E) 11
解法1
设乔伊的年龄为 \( j \) ,克洛伊的年龄为 \( c \) ,已知佐伊的年龄为1。
我们知道必须有9个值 \( k \in \mathbb{Z} \) 使得 \( c + k = a\left( {1 + k}\right) \) ,其中 \( a \) 为整数。
因此, \( c - 1 + \left( {1 + k}\right) = a\left( {1 + k}\right) \) 和 \( c - 1 = \left( {1 + k}\right) \left( {a - 1}\right) \) 。因此,由于 \( k \) 有9个解, \( c - 1 \) 也必须有9个解。我们知道这必须是一个完全平方数。测试完全平方数,我们发现 \( c - 1 = {36} \) ,因此 \( c = {37} \) 。因此, \( j = {38} \) 。现在,由于 \( j - 1 = {37} \) ,根据类似逻辑, \( {37} = \left( {1 + k}\right) \left( {a - 1}\right) \) ,因此 \( k = {36} \) ,乔伊将为 \( {38} + {36} = {74} \) ,其数字之和为 \( \mid \left( \mathrm{E}\right) {11} \) 。
解法2
以上是另一种表述上述解法的方式:
如果一个数同时是Chloe年龄和Zoe年龄的倍数,那么它也是她们年龄差的倍数。由于她们的年龄差不变,这意味着年龄差有9个因数。因此,Chloe与Zoe的年龄差是36,所以Chloe 37岁,Joey 38岁。能同时整除她们年龄的最大公因数是37,因此Joey将会是 \( {74.7} + 4 = \left( E\right) {11} \)
解法3
与上述方法类似,只是解释得更不简洁,更贴近题意(代数味更少)
设 \( C + n \) 表示Chloe的年龄, \( J + n \) 表示Joey的年龄, \( Z + n \) 表示Zoe的年龄,其中 \( n \) 是从现在开始经过的年数。已知 \( C + n \) 恰好有九次是 \( Z + n \) 的倍数。由于 \( Z + n \) 在 \( n = 0 \) 时为1,并将一直增加到大于 \( C - Z \) ,因此它会遍历所有小于 \( C - Z \) 的自然数,包括 \( C - Z \) 的所有因数。为了使 \( C + n \) 是 \( Z + n \) 的整数倍,差值 \( C - Z \) 也必须是 \( Z \) 的倍数,当且仅当 \( Z \) 是 \( C - Z \) 的因数时成立。因此, \( C - Z \) 共有九个因数。最小的具有九个正因数的数是 \( {2}^{2}{3}^{2} = {36} \) (我们希望它尽可能小,以便在Joey的年龄成为Zoe年龄的倍数之前,他的年龄不会达到三位数)。我们还知道 \( Z = 1 \) 和 \( J = C + 1 \) 。因此,
\[ C - Z = {36} \]
\[ J - Z = {37} \]
根据上述逻辑,下一次 \( J - Z \) 是 \( Z + n \) 的倍数时, \( Z + n \) 必须是 \( J - Z \) 的因数。由于37是质数,下一次发生这种情况是在 \( Z + n = {37} \) ,此时 \( J + n = {74.7} + 4 = \) (E)11
2018 AMC 10B 试题/第20题
题目
函数 \( f \) 由 \( f\left( 1\right) = f\left( 2\right) = 1 \) 递归定义,且
\[ f\left( n\right) = f\left( {n - 1}\right) - f\left( {n - 2}\right) + n \]
对所有整数 \( n \geq 3 \) 成立。 \( f\left( {2018}\right) \) 的值是多少?
\( \textbf{(A) }{2016}\;\textbf{(B) }{2017}\;\textbf{(C) }{2018}\;\textbf{(D) }{2019}\;\textbf{(E) }{2020} \)
解法1
\( f\left( n\right) = f\left( {n - 1}\right) - f\left( {n - 2}\right) + n \)
\( = \left( {f\left( {n - 2}\right) - f\left( {n - 3}\right) + n - 1}\right) - f\left( {n - 2}\right) + n \)
\( = {2n} - 1 - f\left( {n - 3}\right) \)
\( = {2n} - 1 - \left( {2\left( {n - 3}\right) - 1 - f\left( {n - 6}\right) }\right) \)
\( = f\left( {n - 6}\right) + 6 \)
因此, \( f\left( {2018}\right) = {2016} + f\left( 2\right) = {2017}.\overset{\not{} }{B} \)
解法2(稍暴力)
先列出数列的前几项。
\[ f\left( 1\right) = 1 \]
\[ f\left( 2\right) = 1 \]
\[ f\left( 3\right) = 3 \]
\[ f\left( 4\right) = 6 \]
\[ f\left( 5\right) = 8 \]
\[ f\left( 6\right) = 8 \]
\[ f\left( 7\right) = 7 \]
\[ f\left( 8\right) = 7 \]
\[ f\left( 9\right) = 9 \]
2018 AMC 10B 试题/第21题
题目
玛丽选择了一个偶数的四位数 \( n \) 。她按从小到大的顺序从左到右写下了 \( n \) 的所有因数: \( 1,2,\ldots ,\frac{n}{2}, n \) 。在某个时刻,玛丽写下了323作为 \( n \) 的一个因数。问:在323右侧写下的下一个因数的最小可能值是多少?
(A) 324 (B) 330 (C) 340 (D) 361 (E) 646
解法1
将323进行质因数分解得到 \( {17} \cdot {19} \) 。所求答案必须是17或19的倍数,因为若不是17或19的倍数,则最小公倍数(LCM)或 \( n \) 的最小可能值将不超过四位数。观察选项, \( \left| {\mathrm{C})\;{340}}\right| \) 是能被17或19整除的最小数字。验证可知 \( n \) 为6460。
解法2
设下一个更大的因数为 \( k \) 。假设 \( \gcd \left( {k,{323}}\right) = 1 \) 。那么,由于 \( {323}\left| {n, k}\right| n \) ,因此 \( {323} \cdot k|n. \) 。然而,因为 \( k > {323} \) , \( {323k} > {323} \cdot {324} > {9999} \) 。因此, \( \gcd \left( {k,{323}}\right) > 1 \) 。注意 \( {323} = {17} \cdot {19} \) 。
因此,最大公约数的最小可能值为17,我们的答案是 \( {323} + {17} = \left( \mathrm{C}\right) {340} \) 。
2018 AMC 10B 第22题
实数 \( x \) 和 \( y \) 独立且均匀地从区间 \( \left\lbrack {0,1}\right\rbrack \) 中随机选取。以下哪个数值最接近 \( x, y, \) 和1作为边长构成钝角三角形的概率?
(A) 0.21 (B) 0.25 (C) 0.29 (D) 0.50 (E) 0.79
解法
勾股不等式告诉我们,在钝角三角形中, \( {a}^{2} + {b}^{2} < {c}^{2} \) 。三角形不等式告诉我们 \( a + b > c \) 。因此,我们有两个不等式:
\[ {x}^{2} + {y}^{2} < 1 \]
\[ x + y > 1 \]
第一个方程是半径为1的圆 \( \frac{1}{4} \) ,第二个方程是从(0,1)到(1,0)的直线。因此,面积为 \( \frac{\pi }{4} - \frac{1}{2} \) ,约为0.29。
解法2
注意,三角形中的钝角必须对着长度恒为1的边。这是因为最大角总是对着最大边,且若三角形有两边为1,则第三边必须大于1才能构成钝角三角形。利用这一观察,我们可以建立余弦定理,其中角对着边1:
\[ {1}^{2} = {x}^{2} + {y}^{2} - {2xy}\cos \left( \theta \right) \]
其中 \( x \) 和 \( y \) 是从 \( \left\lbrack {0,1}\right\rbrack \) 出发的边, \( \theta \) 是对着长度为1的边的角。
通过分离 \( \cos \left( \theta \right) \) ,我们得到:
\[ \frac{1 - {x}^{2} - {y}^{2}}{-{2xy}} = \cos \left( \theta \right) \]
要使 \( \theta \) 为钝角, \( \cos \left( \theta \right) \) 必须为负。因此, \( \frac{1 - {x}^{2} - {y}^{2}}{-{2xy}} \) 为负。由于 \( x \) 和 \( y \) 必须为正, \( - {2xy} \) 必须为负,所以我们必须使 \( 1 - {x}^{2} - {y}^{2} \) 为正。由此,我们可以建立不等式
\[ {x}^{2} + {y}^{2} < 1 \]
此外,为满足三角形的定义,我们需要:
\[ x + y > 1 \]
解应为第一象限中两个方程的重叠部分。
通过观察 \( {x}^{2} + {y}^{2} < 1 \) 是圆的方程,位于第一象限的部分为 \( \frac{\pi }{4} \) 。该直线也可视为一条从(0,1)到(1,0)的弦。通过切去面积为 \( \frac{1}{2} \) 且不属于重叠部分的三角形,我们得到 \( \frac{\pi }{4} - \frac{1}{2} \approx {0.29} \) 。-allenle873
2018 AMC 10B 试题/第23题
有多少对有序正整数(a, b)满足方程
\[ a \cdot b + {63} = {20} \cdot \operatorname{lcm}\left( {a, b}\right) + {12} \cdot \gcd \left( {a, b}\right) , \]
其中 \( \gcd \left( {a, b}\right) \) 表示 \( a \) 和 \( b \) 的最大公约数(greatest common divisor), \( \operatorname{lcm}\left( {a, b}\right) \) 表示它们的最小公倍数(least common multiple)?
(A) 0 (B) 2 (C) 4 (D) 6 (E) 8
解答
设 \( x = \operatorname{lcm}\left( {a, b}\right) \) ,且 \( y = \gcd \left( {a, b}\right) \) 。因此, \( a \cdot b = \operatorname{lcm}\left( {a, b}\right) \cdot \gcd \left( {a, b}\right) = x \cdot y \) 。于是方程变为
\[ x \cdot y + {63} = {20x} + {12y} \]
\[ x \cdot y - {20x} - {12y} + {63} = 0 \]
利用西蒙最爱的因式分解技巧(Simon's Favorite Factoring Trick),我们将方程改写为
\[ \left( {x - {12}}\right) \left( {y - {20}}\right) - {240} + {63} = 0 \]
\[ \left( {x - {12}}\right) \left( {y - {20}}\right) = {177} \]
由于 \( {177} = 3 \cdot {59} \) 且 \( x > y \) ,我们有 \( x - {12} = {59} \) 和 \( y - {20} = 3 \) ,或 \( x - {12} = {177} \) 和 \( y - {20} = 1 \) 。这给出解(71,23)和(189,21)。显然,第一组不成立。假设 \( a > b \) 。我们必须有 \( a = {21} \cdot 9 \) 和 \( b = {21} \) ,然后可以有 \( a < b \) ,因此共有2个解。(avesomeag) 由IronicNinja~编辑
题目
设 \( \underline{ABCDEF} \) 为边长为1的正六边形。分别用 \( X, Y \) 、 \( Z \) 表示边 \( \overline{AB},\overline{CD} \) 、 \( {EF} \) 的中点。由 \( \bigtriangleup {ACE} \) 和 \( \bigtriangleup {XYZ} \) 内部交集构成的凸六边形的面积是多少?
(A) \( \frac{3}{8}\sqrt{3} \) (B) \( \frac{7}{16}\sqrt{3} \) (C) \( \frac{15}{32}\sqrt{3} \) (D) \( \frac{1}{2}\sqrt{3} \) (E) \( \frac{9}{16}\sqrt{3} \)
解法1
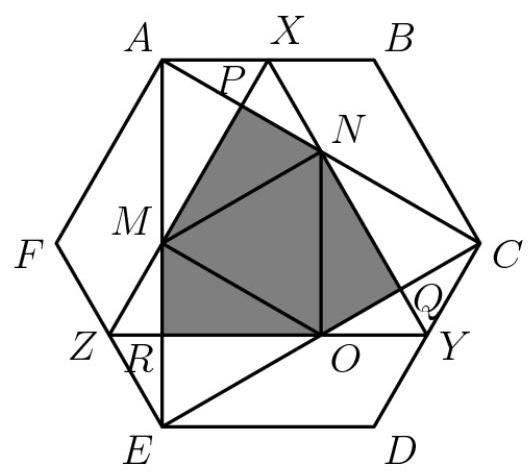
所求面积(六边形 \( {MPNQOR} \) )由一个等边三角形( \( \bigtriangleup {MNO} \) )和三个直角三角形( \( \bigtriangleup {MPN} \) 、 \( \bigtriangleup {NQO} \) 和 \( \bigtriangleup {ORM} \) )组成。
注意到 \( \overline{AD} \) (未画出)与 \( \overline{BC} \) 平行。 \( \overline{XY} \) 将截线 \( \overline{AB} \) 和 \( \overline{CD} \) 分成 \( 1 : 1 \) 的比例,因此它也必须将截线 \( \underline{AC} \) 和截线 \( {CO} \) 分成 \( 1 : 1 \) 的比例。由对称性, \( {CE} \) 与 \( \overline{EA} \) 以及 \( \overline{EM} \) 与 \( \overline{AN} \) 同样适用。
在 \( \bigtriangleup {ACE} \) 中,我们看到 \( \frac{\left\lbrack MNO\right\rbrack }{\left\lbrack ACE\right\rbrack } = \frac{1}{4} \) 和 \( \frac{\left\lbrack MPN\right\rbrack }{\left\lbrack ACE\right\rbrack } = \frac{1}{8} \) 。于是所求面积变为
\[ \left( {\frac{1}{4} + 3 \cdot \frac{1}{8}}\right) \cdot \frac{{\left( \sqrt{3}\right) }^{2} \cdot \sqrt{3}}{4} = \frac{15}{32}\sqrt{3} = C \]
解法2
现在,如果我们观察图形,可以发现我们要求解的六边形的补集由3个等腰梯形( \( {AXFZ} \) 、 \( {XBCY} \) 和 \( {ZYED} \) )和3个直角三角形组成,每个直角三角形的一个直角分别位于 \( X \) 、 \( Y \) 和 \( Z \) 。求梯形面积时,我们知道每个梯形的一条底边就是六边形的边长,为1,另一条底边为3/2(它位于边与最长对角线之间,最长对角线长度为2),高为 \( \frac{\sqrt{3}}{4} \) (利用勾股定理及等腰梯形性质),因此每个梯形面积为 \( \frac{5\sqrt{3}}{16} \) ,总面积为 \( \frac{{15}\sqrt{3}}{16} \) 。(或者,我们也可以先计算六边形 \( {ABCDEF} \) 的面积,再减去 \( \bigtriangleup {XYZ} \) 的面积,如前所述,其边长为3/2)。现在,我们需要求出每个小三角形的面积;若观察顶点在X上的三角形,它与底边为 \( {YC} = 1/2 \) 的三角形相似。利用相似三角形,我们算出底边为1/4,高为 \( \frac{\sqrt{3}}{4} \) ,于是每个三角形面积为 \( \frac{\sqrt{3}}{32} \) ,总面积为 \( 3\frac{\sqrt{3}}{32} \) 。将两部分面积相加,得到 \( \frac{{15}\sqrt{3}}{16} + \frac{3\sqrt{3}}{32} = \frac{{33}\sqrt{3}}{32} \) 。求出总面积,得到 \( 6 \cdot {1}^{2} \cdot \frac{\sqrt{3}}{4} = \frac{3\sqrt{3}}{2} \) 。取补集,得到 \( \frac{3\sqrt{3}}{2} - \frac{{33}\sqrt{3}}{32} = \frac{{15}\sqrt{3}}{32} = \left( C\right) \frac{15}{32}\sqrt{3} \) 。
解法3(三角法)
注意,由两个三角形相交形成的凸六边形的面积,可以通过先求出由三边中点构成的三角形的面积,再减去位于该三角形内部但又在另一三角形外部的区域所形成的小三角形面积来得到。首先,我们求由三边中点构成的三角形的面积。注意,这是一个等边三角形,因此只需求出其边长即可。为此,我们观察位于该三角形之外、外六边形之内的一个等腰梯形。由于正六边形的内角为 \( {120}^{ \circ } \) ,且该梯形为等腰梯形,可知其对角为 \( {60}^{ \circ } \) ,于是该三角形的边长为 \( 1 + 2\left( {\frac{1}{2}\cos \left( {60}^{ \circ }\right) = 1 + \frac{1}{2} = \frac{3}{2}}\right. \) 。因此,该三角形的面积为 \( \frac{\sqrt{3}}{4}{s}^{2} = \frac{9\sqrt{3}}{16} \) 。接下来,我们求这些小三角形的面积。注意,三角形 \( {ACE} \) 从外六边形中截出了若干较小的等腰三角形。这些等腰三角形的底边与前面提到的等腰梯形的底边垂直,因此我们可以利用三角比求出这些小三角形的底和高;由于正六边形具有旋转对称性,这些小三角形全等。于是每个小三角形的面积为 \( \frac{1}{2}\left( \frac{1}{2}\right) \cos \left( {60}^{ \circ }\right) )\left( {\frac{1}{2}\sin \left( {60}^{ \circ }\right) }\right) = \frac{\sqrt{3}}{32} \) ,它们的面积之和为 \( 3 \cdot \frac{\sqrt{3}}{32} = \frac{3\sqrt{3}}{32} \) 。因此,该凸六边形的面积为
\[ \frac{9\sqrt{3}}{16} - \frac{3\sqrt{3}}{32} = \frac{{18}\sqrt{3}}{32} - \frac{3\sqrt{3}}{32} = \left| \frac{{15}\sqrt{3}}{32}\right| \Rightarrow C \]